Research Topics
Research at CEL focuses on the field of robust data communications and digital signal processing as its scientific foundation as well as on communication systems, in particular mobile networks.
In the area of robust data communications and digital signal process, CEL focuses on:
- Efficient, resource-optimized communications
- Channel coding with extremely low error rates for high speed data transmission
- Application of machine learning in telecommunications
- Transmission over channels with nonlinear characteristics
- Software defined and cognitive radios
- Dynamic spectrum management
- Ultra wide band systems
- Digital signal processing and analysis
In the area of mobile communication systems, CEL focuses on:
- Optimization of radio access networks and communicatoin systems using machine learning
- Semantic communication in the context of 6G
- Integration of communication and cyber-physical systems
- Dynamic and self-optimizing/organizing radio access networks
- Multi-modal communication systems and information processing systems
- Application of machine learning to optimize communication protocols, in particular mobile communication protocols
View the research of the CEL on Channel Coding.
Read more
CEL is also working in applications of machine learning in communications.
Read more
Explore the contributions of the CEL in the development of Software Defined Radios.
Read more
Das CEL investigates different aspects of rmobile networks, in particular radio access networks.
Read moreChannel Coding for High Speed Communication
The fundamental problem of communication is that of sending information from one point to another (either in space or time) efficiently and reliably. Examples of communication are the data transmission between a user and a mobile cell tower, between a ground station and a space probe through the atmosphere and free space, the write and read of information on flash memories and hard drives, as well as communication between servers in a data center through optical interconnects. The transmission over the physical medium is subject to noise due to amplification, distortion, and other impairments. As a consequence, the transmitted message may be received with errors.
To reduce the probability of error, Claude E. Shannon showed in his landmark work that with the use of channel coding, the error probability can be made diminishingly small. The principle of channel coding is very simple: to introduce redundancy in the transmitted sequence in a controlled manner such that it can be exploited by the receiver to correct the errors introduced by the channel. This is provided that the rate of the channel code (which determines the overhead added for data protection) is below a quantity called the channel capacity, which is a fundamental limit for any channel.
Today, many channel codes used in practical systems are based on the concept of Low-Density Parity-Check (LDPC) codes. This is mostly due to their good theoretical foundations and the availability of a very fast and simple decoder that can be easily parallelized in a VLSI implementation. LDPC codes were already introduced in the 1960s, but then forgotten due to their large perceived complexity for that time. After the invention of Turbo codes in 1993, a sudden interest in iteratively decodable codes led to the rediscovery of LDPC codes in the 1990s. In the years that followed, a thorough theoretical understanding of LDPC codes was established and LDPC codes were adopted in numerous applications (e.g., WiFi 802.11, DVB-S2, 10G Ethernet (10G-BaseT), 5G mobile communications, and many more).
Channel coding for high-speed communications
In high speed communications over long distances (e.g., optical fibers, optical submarine cables, microwave radio links for connecting remote antenna sites, and many more), we would often like to maximize the coding gain (and hence the data throughput) with still manageable decoding complexity. If a very large coding gain shall be achieved, LDPC codes are still a good choice due to their well-understood error correction properties and the availability of a massively parallel decoder. However, we would like to increase the coding gain even further.
About two decades ago, LDPC convolutional codes were introduced. These codes superimpose LDPC codes with a convolutional structure. The initial goal was to combine the advantages of both convolutional and LDPC codes and the resulting codes were called LDPC convolutional codes. A similar idea was already pursued in the late 1950s and early 1960s with the concept of recurrent codes. The full potential of LDPC convolutional codes was not realized until a few years later, when it was realized that the performance of some LDPC convolutional code constructions asymptotically approaches the performance of optimum maximum likelihood decoding. For investigating this effect, a slightly modified construction called "spatially coupled codes" was introduced. In the following, we restrict ourselves to using this latter term. The main advantage of spatially coupled codes is that very powerful codes can be constructed which can be decoded with a simple windowed decoder. Therefore, spatially coupled LDPC codes (SC-LDPC Codes) can be considered prime candidate for increasing the coding gains in high-speed communication systems.
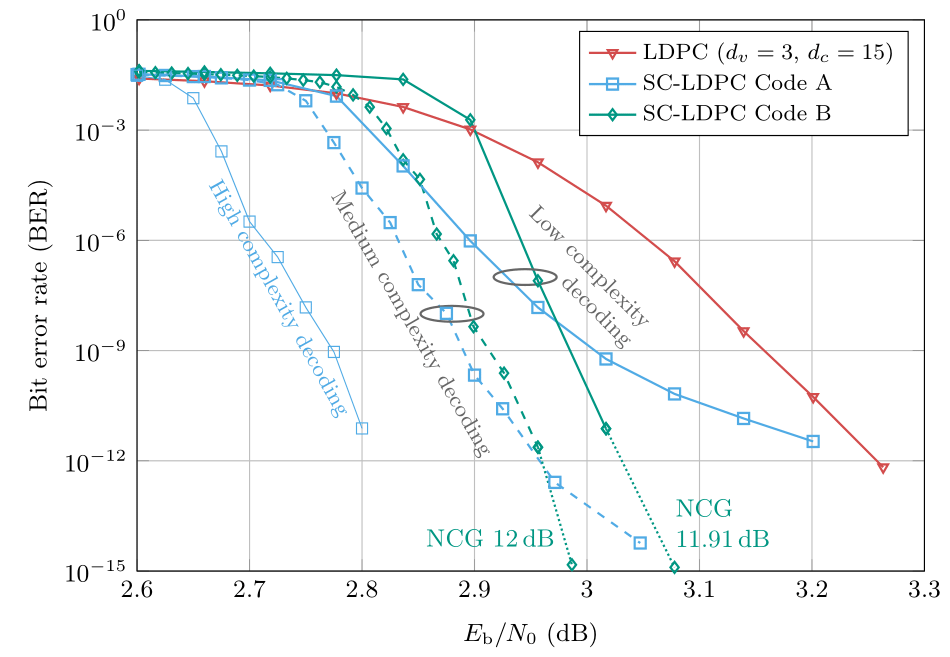
The following picture shows the bit error rate obtained by two SC-LDPC codes compared with a conventional LDPC code often used if low error rates are targeted. All codes have the same rate of 0.8, which corresponds to an overhead of 25% for parity bits. With low-complexity windowed decoding, which has roughly the same complexity than standard LDPC decoding, we can already achieve a significant gain compared with the LDPC code. The main advantage of SC-LDPC codes is that they are future-proof. Increasing the complexity will lead to larger coding gains. This favors their use in communication standards, such that with a given standardized and backwards compatible system, larger gains will be available if the VLSI performance increases in the future or if better decoders become available. We can also note that at a bit error rate of 10-15, we are within 1dB of the Shannon limit with an implementation that uses finite precision arithmetic.
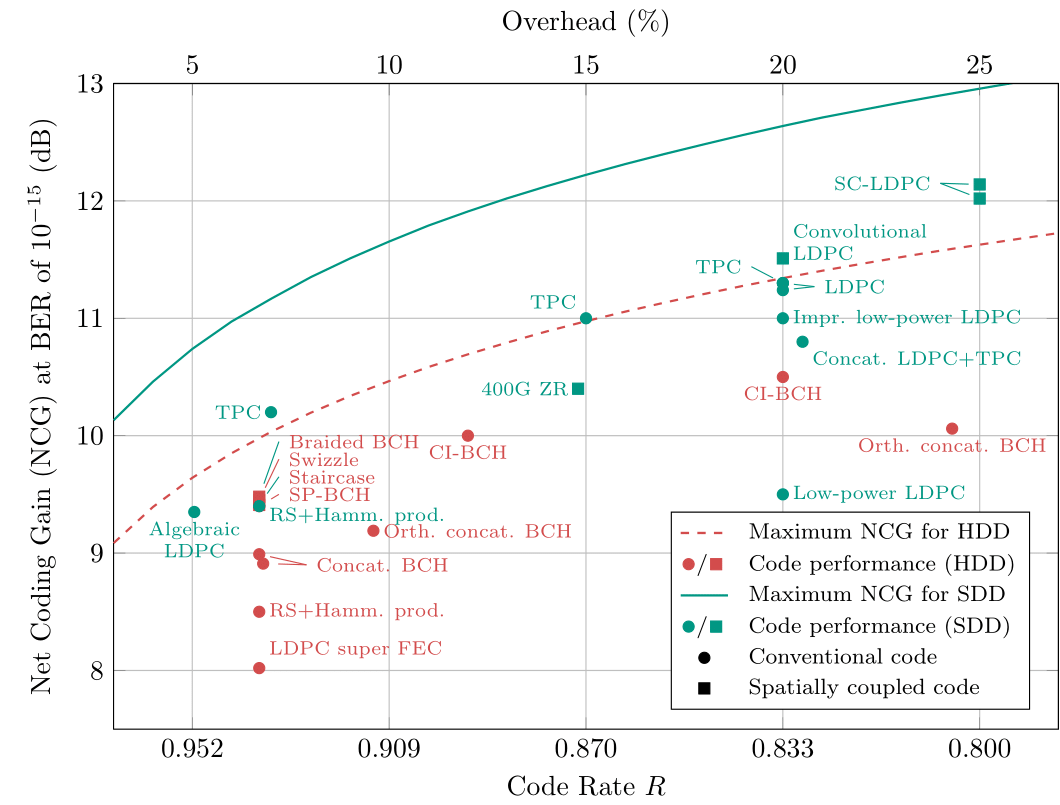
The following picture shows the net coding gains of some channel coding schemes used in optical communication systems, a prime example of a high-speed communication system. We distinguish between channel codes with hard-decision decoding (HDD), which are usually designed for low-complexity transceivers and channel codes with soft-decision decoding (SDD), which are usually designed for high-performance transceivers. Square markers indicate the schemes where spatially coupled codes are used. The most powerful coding schemes that are currently being used belong to the class of spatially coupled codes. In particular the SC-LDPC Codes A and B shown above deliver best in class performance.
Channel coding research at CEL
At CEL, we carry out fundamental research on channel coding for high-speed communication systems. We intend to develop new coding schemes suited for low-complexity decoding and delivering best possible coding gains. We aim at low error floors and consider peculiarities of the transmission system, e.g., optical channels, or microwave backhaul channels. Besides spatially coupled codes, we continue to assess other possible coding schemes depending on the application.
Related literature
- V. Aref, N. Rengaswamy and L. Schmalen, "Finite-Length Analysis of Spatially-Coupled Regular LDPC Ensembles on Burst-Erasure Channels", IEEE Transactions on Information Theory, vol. 64, no. 5, pp. 3431-3449, May 2018 [IEEE Xplore] [preprint on arXiv]
- L. Schmalen, V. Aref, J. Cho, D. Suikat, D. Rösener, and A. Leven, "Spatially Coupled Soft-Decision Forward Error Correction for Future Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 33, no. 5, pp. 1109-1116, March 2015 [IEEE Xplore]
- L. Schmalen, D. Suikat, D. Rösener, V. Aref, A. Leven, and S. ten Brink, "Spatially Coupled Codes and Optical Fiber Communications: An Ideal Match?", IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Special Session on Signal Processing, Coding, and Information Theory for Optical Communications, Stockholm, Sweden, June 2015 [IEEE Xplore] [preprint on arXiv]
- A. Leven and L. Schmalen, "Status and Recent Advances on Forward Error Correction Technologies for Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 32, no. 16, pp. 2735-2750, Aug. 2014 [IEEE Xplore]
Machine Learning in Communications
In recent years, systems with the ability to learn drew wide attention in almost every field. Among many in the past decade, image and big data processing have been boosted tremendously by machine learning (ML)-based techniques, an artificial intelligence (AI) has beaten the world’s best chess or GO players, and specific neural networks are able to unfold proteins.
Traditional communication systems have managed to reach the fundamental limits of communications devised over 70 years ago by Claude Elwood Shannon, for some specific scenarios. However, for a large breadth of applications and scenarios, we either do not have sufficiently simple models enabling the design of optimal transmission systems or the resulting algorithm are prohibitively complex and computationally intense for low-power applications (e.g., Internet-of-Things, battery-driven receivers). The rise of machine learning and the advent of powerful computational resources have brought many novel potent numerical software tools, which enable the optimization of communication systems by reducing complexity or solving problems that could not be solved using traditional methods.
At the CEL, we carry out research on machine learning algorithms for optimization in communications. Basic work includes the model identification of a communication engineering problem, its conversion to an optimization problem and acquisition of data sets for training and evaluation. We are currently working on multiple projects, for example nonlinearity compensation in optical fiber communication systems, the design of novel modulation formats for short-reach optical communications, digital predistortion of nonlinear radio power amplifiers, blind channel estimation and equalization, and low-complexity channel decoding. In what follows, we will briefly describe some of these topics.
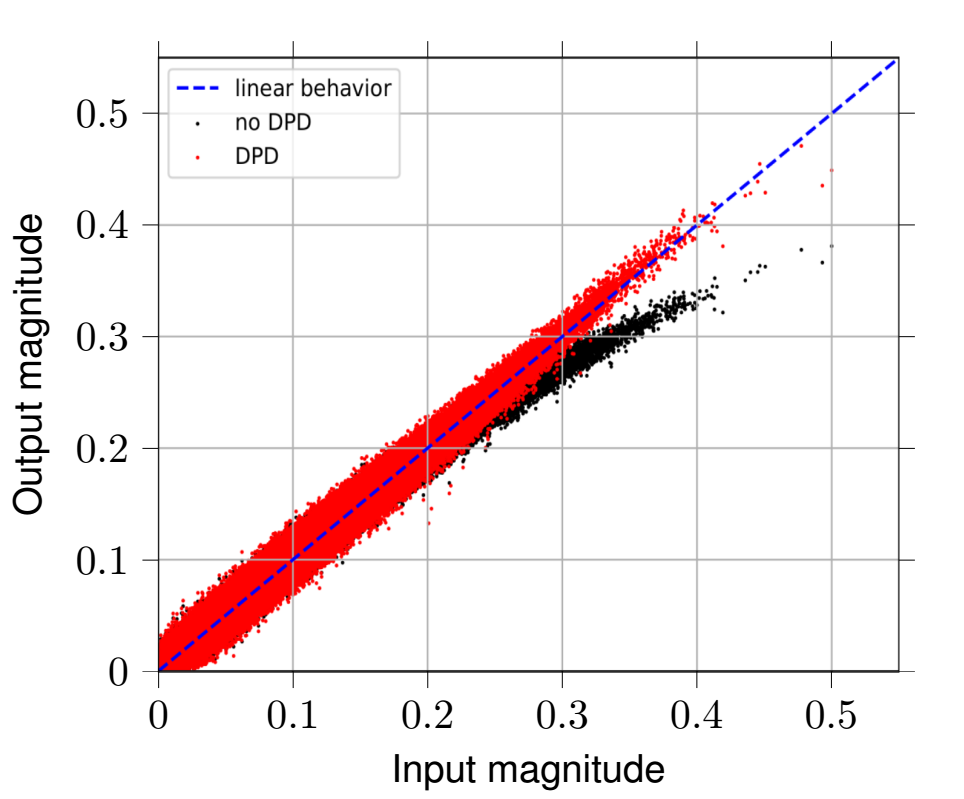
Combating the influence of system nonlinearities is an essential task not only, but especially in OFDM-systems, which inherently exhibit high Peak-to-Average Power Ratios (PAPR). This can drive radio power amplifiers into their nonlinear behavior, resulting in amplitude and phase distortions. Depending on the system bandwidth, the power amplifier introduces additional memory effects, which further degrades the system’s performance. In order to linearize the system, a Digital Predistortion (DPD) scheme can be designed and placed upstream the radio power amplifier. Unfortunately, higher bandwidths and cost-efficient radio power amplifiers intensify memory effects as well as amplitude and phase distortion, so conventional DPD (e.g., using Volterra series) are becoming exorbitantly complex and computationally intense. To overcome these issues, we designed a fast-adapting DPD based on feed-forward neural networks and tested the system using Software Defined Radios (SDRs). Figure 1 depicts the DPD’s performance for magnitude linearization. The predistorted time-domain OFDM-samples show linear behavior, whereas non-predistorted OFDM time-domain samples experience nonlinear distortion.
Commonly, channel equalization is conducted by non-blind adaptive algorithms which require known pilot symbols within the transmit sequence and, thus, lose data rate. Since communication systems become more and more optimized, there is a strong demand for blind equalizers which may approach maximum likelihood performance. Although there is a bunch of proposed schemes, basically there is only one applicable optimal algorithm for the special case of constant modulus (CM) modulation formats (e.g., M-PSK). Other schemes mainly suffer poor convergence rates, high implementation complexities, and sub-optimal criteria.
At the CEL, we analyze novel approaches based on unsupervised deep learning, which potentially approach maximum likelihood performance. Since its functionality differs from the classical digital signal processing (DSP) blocks, we have to develop metrics and environments for fair comparison. Also, some common ML issues, such as limited training sets, do not apply to communications, so adaptions may be reasonable.
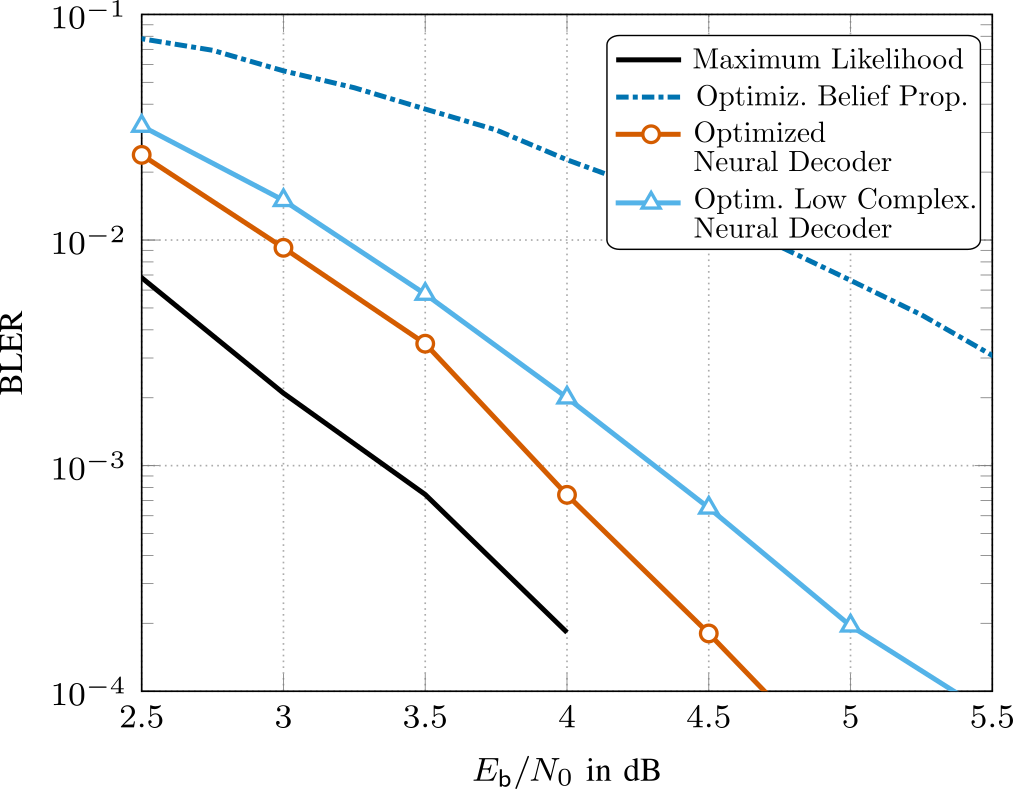
For short channel codes, such as BCH, Reed-Muller and Polar codes, achieving close to maximum likelihood decoding performance using conventional methods is computationally complex. Fueled by the advances in the field of deep learning, belief propagation (BP) decoding can also be formulated in the context of deep neural networks. In BP decoding, messages are passed through unrolled iterations in a feed-forward fashion. Additionally, weights can be introduced
at the edges, which are then optimized using stochastic gradient descent (and variants thereof). This decoding method is commonly referred to as neural belief propagation and can be seen as a generalization of BP decoding, where all messages are scaled by a single damping coefficient. However, the weights add extra decoder complexity. Additionally, in order to achieve competitive performance, overcomplete parity-check matrices are necessary, which further increase decoding complexity. In our research [1], we have employed pruning techniques from ML to significantly reduce decoder complexity and have jointly optimized quantizers for the messages, such that the resulting decoders are directly ready for hardware implementation. The results are shown in Fig. 2, where we see that our optimized decoder operates within 0.5 dB from ML performance. More details can be found in [1].
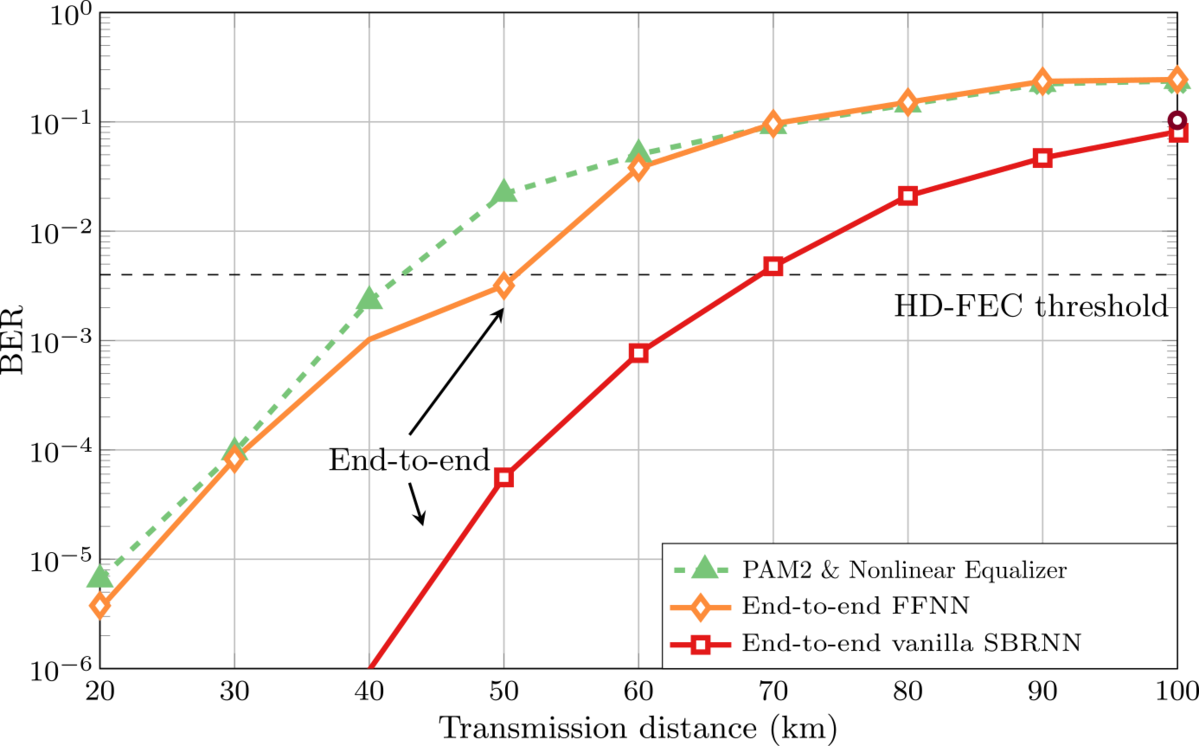
For the design of short-reach optical communication systems based on intensity modulation with direct detection (IM/DD), we may interpret the complete communication chain from the transmitter input to the receiver output as a single neural network and optimize its parameters yielding optimal end-to-end communication performance. In such systems, the combination of chromatic dispersion, introduced inter-symbol interference (ISI), and nonlinear signal detection by a photodiode imposes severe limitations. We have investigated multiple approaches for designing the neural networks [2], [3], including feed-forward and recurrent neural networks. We have shown experimentally that our networks can outperform pulse amplitude modulation (PAM) with conventional linear and nonlinear equalizers (e.g., based on Volterra filters). We have additionally employed Generative Adversarial Networks (GANs) to approximate experimental channels [4]. In Fig. 3, we exemplarily show the bit error rate performance of three such systems (conventional PAM with nonlinear equalizer and two different end-to-end optimized transceivers), where we can observe gains in the range of 20-25km at the FEC threshold.
References
[1] A. Buchberger, C. Häger, H. D. Pfister, L. Schmalen, and A. Graell i Amat, “Pruning Neural Belief Propagation Decoders,” IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, Jun. 2020
[2] B. Karanov, M. Chagnon, F. Thouin, T. A. Eriksson, H. Bülow, D. Lavery, P. Payvel and L. Schmalen, “End-to-end Deep Learning of Optical Fiber Communications,” IEEE/OSA Journal of Lightwave Technology, vol. 36, no. 20, pp. 4843-4855, Oct. 2018, also available as arXiv:1804.04097
[3] B. Karanov, M. Chagnon, V. Aref, F. Ferreira, D. Lavery, P. Bayvel, and L. Schmalen, “Experimental Investigation of Deep Learning for Digital Signal Processing in Short Reach Optical Fiber Communications,” IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, Oct. 2020 (also available on https://arxiv.org/abs/2005.08790)
[4] B. Karanov, M. Chagnon, V. Aref, D. Lavery, P. Bayvel, and L. Schmalen, “Concept and Experimental Demonstration of Optical IM/DD End-to-End System Optimization using a Generative Model,” Optical Fiber Communications Conference (OFC), San Diego, CA, USA, paper Th2A.48, Mar. 2020
Mobile Networks
In the course of the development of the 5th generation of the mobile radio standard 3GPP, significant innovations were introduced. The most notable innovations are the flexible scalability of the physical transmission layer, the use of frequencies in the millimeter range and the revised design of the core network. The physical layer of the 5G standard enables symbol durations of different lengths, which means that a wide range of applications with extreme requirements in terms of latency and data throughput can be supported. By using higher frequencies in the millimeter range, it is possible to use significantly higher bandwidths and achieve a much higher data throughput. However, this is only possible by using multiple-antenna systems with a large number of antennas, which require a fine-granular control. All system functions have been redefined in the core network, new concepts such as the separation of control and data plane and virtualization have been implemented, and the core network can integrate various wired and wireless access technologies.
In the field of mobile communications networks, the CEL investigates the system context of mobile communications, i.e. how modern communications algorithms can be integrated into the system, how the necessary data for operating the algorithms can be provided, what interactions there are in the overall system and how the network architecture must change, to support these algorithms. The following subject areas receive special attention.
Optimization of wireless networks and communication systems using machine learning
In the context of 5G, the (standardized) use of AI algorithms in mobile networks was discussed for the first time. At the CEL, we are researching how communications engineering processes can be improved using AI algorithms, e.g. channel coding or channel equalizers. On the other hand, we research how the operation of mobile networks can be optimized with the help of AI algorithms, e.g. mobility processes or communication protocols. In addition to the actual algorithms, we examine how the necessary data can be collected and stored.
Dynamic and self-optimizing wireless networks
With the constantly increasing demand on mobile networks, the structures and methods used are also becoming more and more complex, which means that the operation and optimization of the network has to be automated and adapted to the application scenario. For this purpose, the CEL is investigating how the mobile network can dynamically adapt to the requirements, e.g. flexible topologies (drone-supported networks) and resilient structures both in the radio access network and in the core network.
Multi-modal communication and information processing systems
Cellular networks are now more closely linked to specific applications, e.g. automobiles or IoT. As a result, information from different domains apart from mobile communications becomes relevant, e.g. radar measurements or video recording. The CEL investigates how this information can be used to optimize the operation of a mobile network jointly with the application layer, e.g. in the automated remote control of robots.
Integration of communication and cyber-physical systems
With the 5G standard, applications that have extreme requirements in terms of latency and reliability were also given greater consideration. In addition to the quality of service on the radio interface, the integration into the entire mobile radio system, including the core network and the application, is of essential importance, because latency and reliability are dominated by the "weakest" link in the overall transmission path. The CEL is researching how the integration of the various mobile radio domains with applications or end-to-end requirements can be implemented.
Software Defined Radio and Cognitive Radio
The vision behind software radio is to realize a radio’s communication specific signal processing, e.g. modulation, channel equalization and channel coding, as far as possible in software. Ideally, customized hardware could be replaced by a general purpose processor with D/A- and A/D-converters and amplifiers. This allows for highly flexible usage of the hardware, as signal processing is carried out as algorithms on the general pupose processor.
The CEL has been continuously involved in SDR projects since 1996. Based on this experience, CEL is now pursuing the evolution of software radios towards cognitive radios. Cognitive radios are self-learning intelligent software radios which are able to monitor their environment and to adapt to the actual conditions such as standards, channel properties, etc.
Due to the vast software and hardware infrastructure available at the CEL, multiple research projects in the scope of software and cognitive radios are possible. Models and algorithms can be investigated using simulations. We have access to large software libraries to describe transmission systems. Additionally, the available hardware - Universal Software Radio Peripherals (USRPs) from Ettus Research - allow testing and experiment validation of the algorithms.