Forschungsgebiete
Die Forschung am CEL fokussiert sich auf den Bereich der robusten Datenübertragung und der sie beherrschenden Digitalen Signalverarbeitung sowie auf den Bereich der Kommunikationsnetze und im Besonderen der Funknetzwerke.
Im Bereich robusten Datenübertragung und digitalen Signalverarbeitung wird an folgenden Themen gearbeitet:
- Effiziente, ressourcenoptimierte Übertragung
- Kanalcodierung mit extrem niedrigen Fehlerrate für die Hochgeschwindigkeitsdatenübertragung
- Anwendung maschinellem Lernen in der Nachrichtentechnik
- Übertragung über Kanäle mit nichtlinearen Eigenschaften
- Software-Defined und Cognitive Radios
- Dynamisches Spektrumsmanagement
- Ultra-Wide-Band-Systeme
- Digitale Funksignalverarbeitung und -analyse
Im Bereich nachrichtentechnischer Systeme wird an folgenden Themen gearbeitet:
- Optimierung von Funknetzwerken und Kommunikationssystemen mit Hilfe von maschinellem Lernen
- Semantische Kommunikation im Kontext von 6G
- Integration von Kommunikationssystemen und Cyber-Physical Systemen
- Dynamische und selbst-optimierende Funknetzwerke
- Multi-modale Kommunikationssysteme und informationsverarbeitende Systeme
- Anwendung maschinellen Lernens zur Optimierung von Kommunikationsprotokollen, im Besonderen Mobilfunkprotokolle
Passend zu den verfolgten Forschungsthemen werden Kooperationen in nationalen (BMBF, DFG) und europäischen Förderprogrammen gesucht. Gemeinsame Projekte mit der Industrie und mit öffentlichen Auftraggebern runden die kreative wissenschaftliche Arbeit ab.
Erfahren Sie mehr über die Forschungsarbeit des CEL im Bereich der Kanalcodierung.
Mehr lesen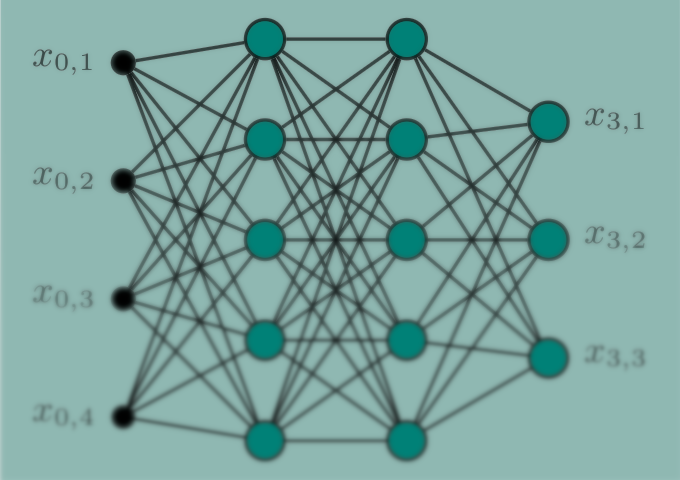
Auch im Bereich der Anwendung von Machine Learning im Bereich der Nachrichtentechnik forscht das CEL.
Mehr lesen
Entdecken Sie die Beiträge des CEL zur Entwicklung von Software Defined Radios.
Mehr Lesen
Das CEL untersucht verschiedene Aspekte von Mobilfunknetzen.
Mehr lesenKanalcodierung für die Hochgeschwindigkeitskommunikation
Das fundamentale Problem der Nachrichtentechnik ist es, Information effizient und zuverlässig von einem Punkt (im Raum oder in der Zeit) zu einem anderen Punkt zu transportieren. Beispiele von Systemen der Nachrichtentechnik sind die mobile Kommunikation zwischen Smartphone-Nutzer und Mobilfunkmast, Datenübertragung zwischen Satellit und Bodenstation durch die Atmosphäre und den freien Raum, das Speicher und Lesen von Information in Flash-Speichern und Festplatten, sowie die Vernetzung von Servern in Datenzentren mittels Kupfer- und Glasfaserkabel. Die Übertragung der Daten über ein physikalisches Medium ist unwiederbringlich durch Rauschen (z.B. thermisches Rauschen in Verstärkern) und andere Effekte gestört. Als Konsequenz dieses Rauschens und der Verzerrungen ist das Empfangssignal fehlerhaft.
Um die Fehlerwahrscheinlichkeit zu verringern hat Claude E. Shannon in seiner bahnbrechenden Arbeit gezeigt, dass mithilfe einer sogenannten Kanalcodierung die Fehlerwahrscheinlichkeit beliebig klein werden kann, falls bestimmte Bedingungen erfüllt sind. Das Prinzip der Kanalcodierung ist einfach: Es wird in einer wohldefinierten Art und Weise Redundanz dem Sendesignal hinzugefügt. Diese Redundanz kann am Empfänger gezielt verwendet werden um die durch die Übertragung verursachten Übertragungsfehler zu korrigieren. Dazu muss die Rate des Kanalcodes (diese definiert die Menge an zugefügter Redundanz) unterhalb einer von Shannon eingeführten Größe - der Kanalkapazität - sein. Die Kanalkapazität ist eine fundamentale Größe eines jeden Kanals.
Heutzutage existieren leistungsfähige Kanalcodierverfahren. Die meisten dieser Verfahren basieren auf der Klasse der sogenannten Low-Density Parity-Check (LDPC) Codes. LDPC-Codes wurden schon in den 1960er Jahren eingeführt, sind danach aber weitestgehend in Vergessenheit geraten, da ihre Decodierung für die damaligen Verhältnisse zu aufwändig war. Nach der Erfindung von Turbo-Codes im Jahre 1993 gab es ein neu erwecktes Interesse an iterativ decodierbaren Codes, und die LDPC-Codes wurden wiederentdeckt. In den darauffolgenden Jahren konnte ein tiefgehendes und gründliches Verständnis dieser Codes erarbeitet werden und neue, sehr schnelle und hochparallelisierbare Decodierverfahren wurden entwickelt. Aus diesen Gründen werden LDPC-Codes heute in vielen Anwendungen, wie WiFi 802.11, DVB-S2, 10G Ethernet (10G-BaseT), sowie 5G als Methode der Wahl verwendet.
Kanalcodierung für die Hochgeschwindigkeitsdatenübertragung
In der Hochgeschwindigkeitsdatenübertragung über lange Distanzen (z.B. Glasfaserunterseekabel, optische Glasfasern für das Kernnetz, Mikrowellenverbindungen zur Anbindung entlegener Antennen u.v.m) soll vielfach der erreichbare Codiergewinn (und damit auch der Datendurchsatz) maximiert werden bei gleichzeitig niedriger Decodierkomplexität. Soll ein möglichst hoher Codiergewinn angestrebt werden, sind LDPC-Codes auch in dieser Anwendung eine gute Wahl aufgrund ihrer gut untersuchten theoretischen Eigenschaften und der Verfügbarkeit massiv paralleler Decodierverfahren. Allerdings können LDPC-Codes nie den maximal möglichen Codiergewinn erzielen aufgrund Limitierungen in ihrer Konstruktion.
Vor ungefähr 2 Jahrzehnten wurden LDPC-Faltungscodes eingeführt. Diese Codes verbinden LDPC-Codes mit einer übergeordneten Faltungsstruktur. Die Ursprungsidee war die Kombination der Vorteile von LDPC-Codes und Faltungscodes. Eine ähnliche Idee wurde schon in den 1950er und 1960er Jahren mit dem Konzept rekurrenter Codes verfolgt. Das volle Potential dieser LDPC-Faltungscodes ist erst vor einigen Jahren zum Vorschein gekommen, als realisiert wurde, dass die Leistungsfähigkeit dieser Codes asymptotisch die gleiche Leistungsfähigkeit wie ein optimaler (maximum likelihood) Decoder aufweist. Zur Analyse dieses Effekts wurde eine leicht veränderte Konstruktion eingeführt. Die resultierenden Codes wurden "räumlich verkettete" (engl. spatially coupled) Codes genannt. Der Hauptvorteil dieser Codes ist die Möglichkeit, sehr leistungsfähige Codes zu konstruieren, die nichtsdestotrotz mit einem sehr einfachen gefensterten Decoder decodiert werde können. Aus diesem Grund sind räumlich verkettete LDPC-Codes (SC-LDPC-Codes) erstklassige Kandidaten für zukünftige Hochgeschwindigkeitskommunikationssysteme mit sehr hohen Codiergewinnen.
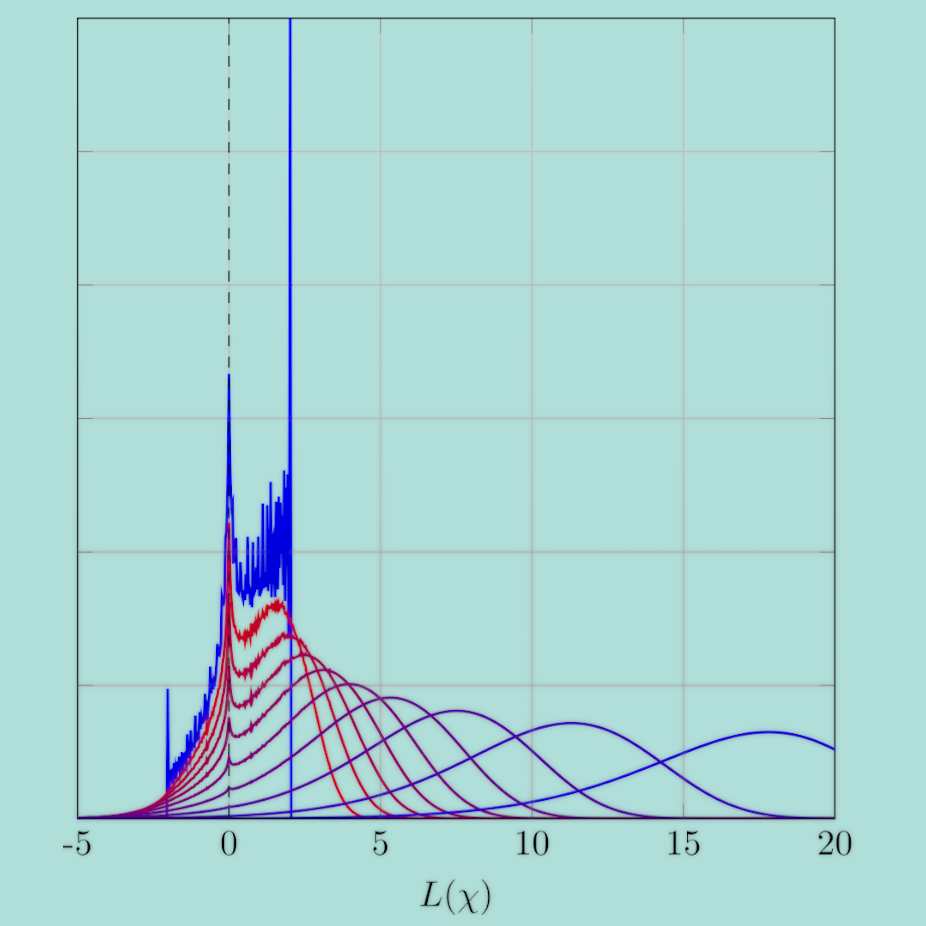
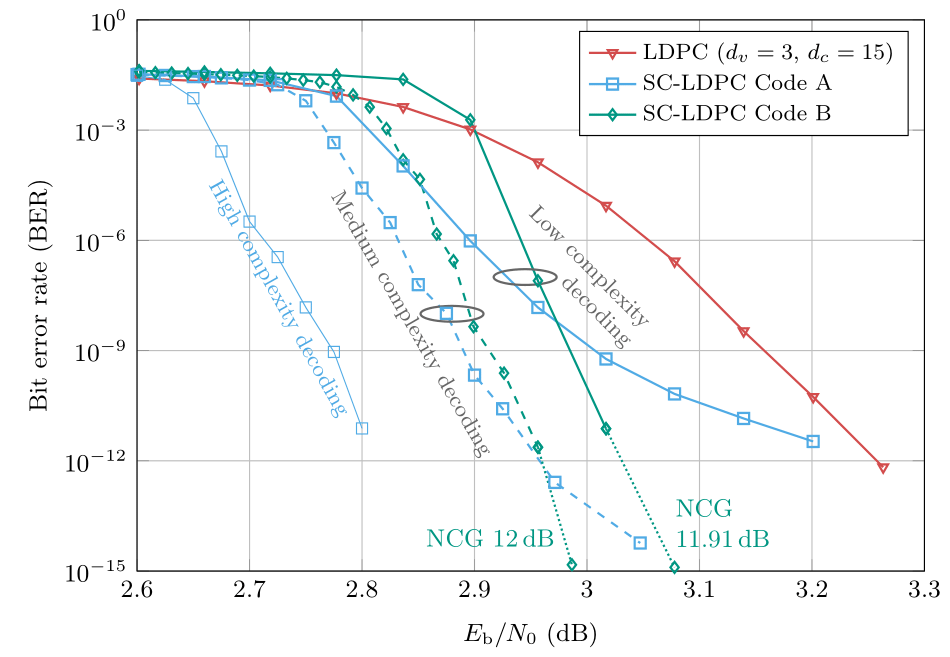
Das folgende Bild zeigt die Fehlerrate (als Funktion über das Signal-Rausch-Verhältnis), die mit zwei SC-LDPC-Codes erzielt werden kann, im Vergleich mit einem herkömmlichen LDPC-Codes, wie er oft verwendet wird. Alle Codes besitzen eine Rate von 0.8 (dies entspricht einem Overhead von 25% für die Redundanzinformation). Mit einem gefensterten Decoder niedriger Komplexität (dieser weist ungefähr die gleiche Komplexität wie ein LDPC-Decoder auf) kann schon ein signifikanter Codiergewinn gegenüber LDPC-Codes erzielt werden. Ein weiterer Vorteil von SC-LDPC-Codes ist deren Zukunftssicherheit. Ein Erhöhen der Decodierkomplexität führt zu zusätzlichen Gewinnen. Dies ist ein weiteres Argument für deren Einsatz in zukünftigen Nachrichtensystemen: mit einem standardisierten und somit rückwärtskompatiblen Verfahren können in der Zukunft höhere Gewinne erzielt werden, wenn die Möglichkeiten der VLSI-Implementierung die Implementierung komplexerer Decoder erlauben. Wir können auch feststellen dass bei einer Bitfehlerrate von ungefähr 10-15 diese Codes (mit einer Festkommaimplementierung) die von Shannon postulierte Kanalkapazität bis auf unter 1dB annähern.
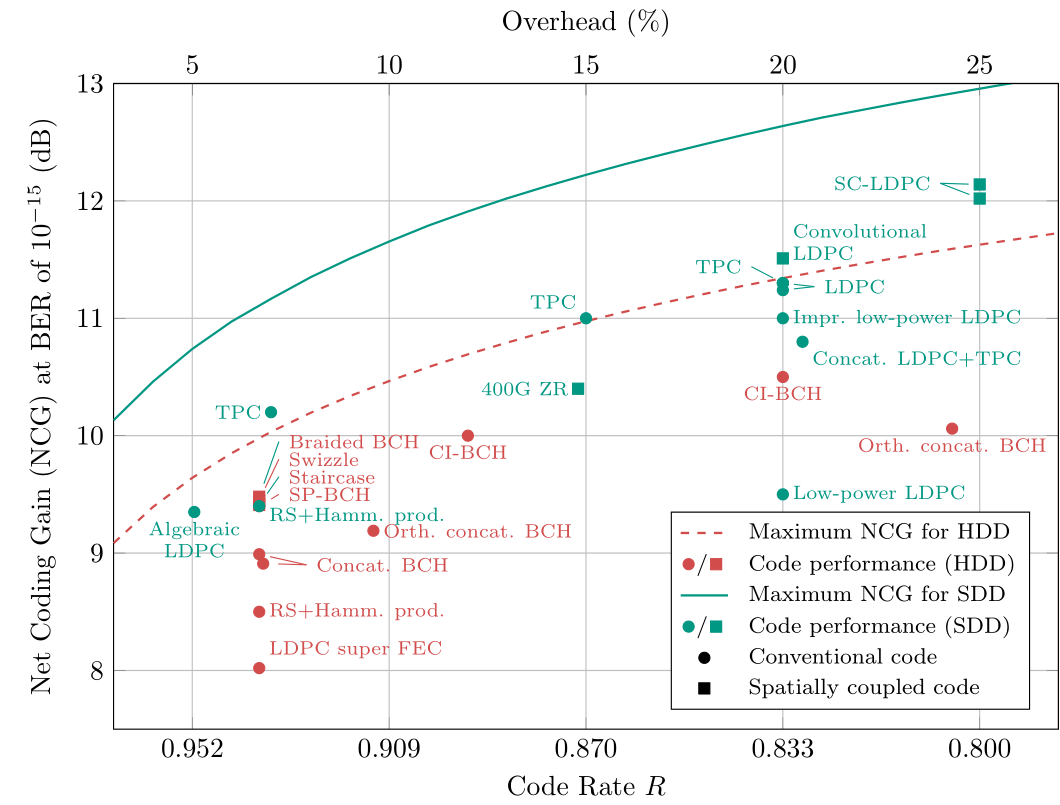
Im folgenden Bild sind die Codiergewinne (sowie deren theoretische Grenzen) für einige Kanalcodierverfahren, wie sie in optischen Nachrichtensystemen verwendet werden, aufgezeigt. Wir unterscheiden zwischen Codes mit Hard-Decision Decodierung (HDD, üblicherweise entworfen für Systeme mit niedriger Empfängerkomplexität) und Codes mit Soft-Decision Decodierung (SDD, üblicherweise entworfen für Systeme mit hohen Codiergewinnen). Eckige Symbole markieren räumlich verkettete Codes. Wir stellen fest, dass die meisten der leistungsfähigsten Codierverfahren solche mit räumlich verketteten Codes sind. Insbesondere SC-LDPC-Codes A und B aus dem vorangegangenen Beispiel haben die höchsten Gewinne.
Forschung zu Kanalcodierung am CEL
Am CEL beschäftigen wir uns mit fundamentalen Fragestellungen zur Kanalcodierung für Hochgeschwindigkeitsdatenübertragungssysteme. Wir entwickeln neue Codierverfahren für niedrige Decodierkomplexität und trotzdem hohen Codiergewinnen. Wir wollen dabei möglichst die Fehlerrate minimieren und berücksichtigen die Eigenschaften des zugrundeliegenden Übertragungssystems, z.B. optische Kanäle oder Mikrowellenlinks. Neben räumlich verketteten Codes untersuchen wir auch die Möglichkeiten alternativer Verfahren, je nach zugrundeliegender Anwendung.
Ausgewählte Literatur:
V. Aref, N. Rengaswamy and L. Schmalen, "Finite-Length Analysis of Spatially-Coupled Regular LDPC Ensembles on Burst-Erasure Channels", IEEE Transactions on Information Theory, vol. 64, no. 5, pp. 3431-3449, May 2018 [IEEE Xplore] [preprint auf arXiv]
L. Schmalen, V. Aref, J. Cho, D. Suikat, D. Rösener, and A. Leven, "Spatially Coupled Soft-Decision Forward Error Correction for Future Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 33, no. 5, pp. 1109-1116, March 2015 [IEEE Xplore]
L. Schmalen, D. Suikat, D. Rösener, V. Aref, A. Leven, and S. ten Brink, "Spatially Coupled Codes and Optical Fiber Communications: An Ideal Match?", IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Special Session on Signal Processing, Coding, and Information Theory for Optical Communications, Stockholm, Sweden, June 2015 [IEEE Xplore] [preprint auf arXiv]
A. Leven and L. Schmalen, "Status and Recent Advances on Forward Error Correction Technologies for Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 32, no. 16, pp. 2735-2750, Aug. 2014 [IEEE Xplore]
Machine Learning in Communications
In recent years, systems with the ability to learn drew wide attention in almost every field. Among many in the past decade, image and big data processing have been boosted tremendously by machine learning (ML)-based techniques, an artificial intelligence (AI) has beaten the world’s best chess or GO players, and specific neural networks are able to unfold proteins.
Traditional communication systems have managed to reach the fundamental limits of communications devised over 70 years ago by Claude Elwood Shannon, for some specific scenarios. However, for a large breadth of applications and scenarios, we either do not have sufficiently simple models enabling the design of optimal transmission systems or the resulting algorithm are prohibitively complex and computationally intense for low-power applications (e.g., Internet-of-Things, battery-driven receivers). The rise of machine learning and the advent of powerful computational resources have brought many novel potent numerical software tools, which enable the optimization of communication systems by reducing complexity or solving problems that could not be solved using traditional methods.
At the CEL, we carry out research on machine learning algorithms for optimization in communications. Basic work includes the model identification of a communication engineering problem, its conversion to an optimization problem and acquisition of data sets for training and evaluation. We are currently working on multiple projects, for example nonlinearity compensation in optical fiber communication systems, the design of novel modulation formats for short-reach optical communications, digital predistortion of nonlinear radio power amplifiers, blind channel estimation and equalization, and low-complexity channel decoding. In what follows, we will briefly describe some of these topics.
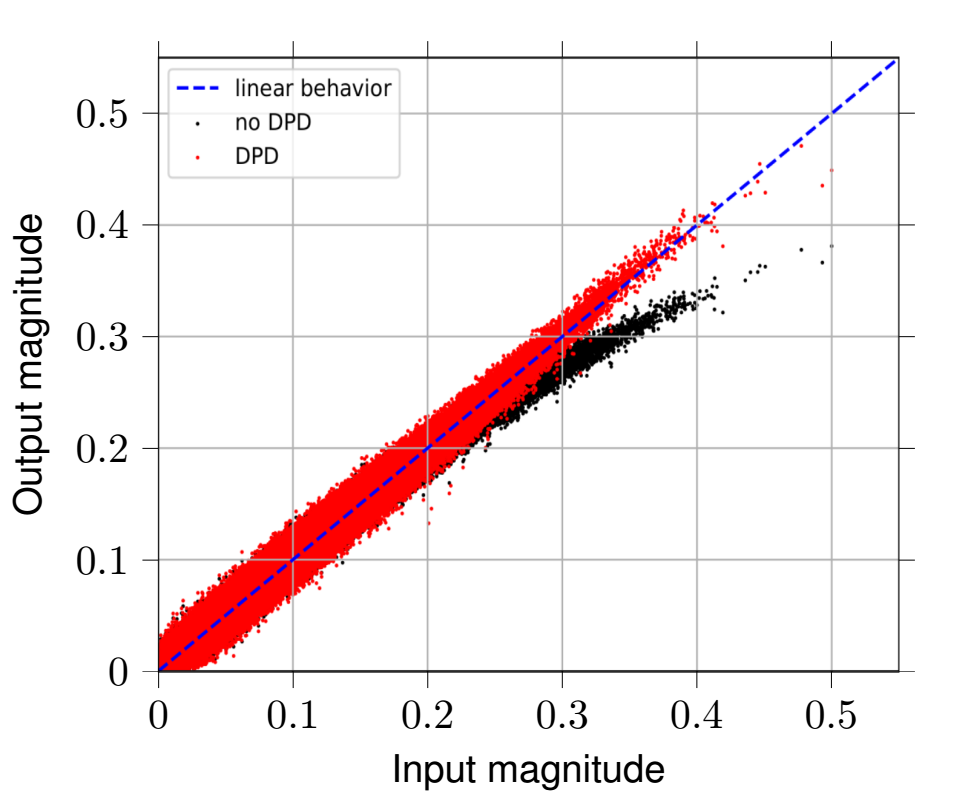
Combating the influence of system nonlinearities is an essential task not only, but especially in OFDM-systems, which inherently exhibit high Peak-to-Average Power Ratios (PAPR). This can drive radio power amplifiers into their nonlinear behavior, resulting in amplitude and phase distortions. Depending on the system bandwidth, the power amplifier introduces additional memory effects, which further degrades the system’s performance. In order to linearize the system, a Digital Predistortion (DPD) scheme can be designed and placed upstream the radio power amplifier. Unfortunately, higher bandwidths and cost-efficient radio power amplifiers intensify memory effects as well as amplitude and phase distortion, so conventional DPD (e.g., using Volterra series) are becoming exorbitantly complex and computationally intense. To overcome these issues, we designed a fast-adapting DPD based on feed-forward neural networks and tested the system using Software Defined Radios (SDRs). Figure 1 depicts the DPD’s performance for magnitude linearization. The predistorted time-domain OFDM-samples show linear behavior, whereas non-predistorted OFDM time-domain samples experience nonlinear distortion.
Commonly, channel equalization is conducted by non-blind adaptive algorithms which require known pilot symbols within the transmit sequence and, thus, lose data rate. Since communication systems become more and more optimized, there is a strong demand for blind equalizers which may approach maximum likelihood performance. Although there is a bunch of proposed schemes, basically there is only one applicable optimal algorithm for the special case of constant modulus (CM) modulation formats (e.g., M-PSK). Other schemes mainly suffer poor convergence rates, high implementation complexities, and sub-optimal criteria.
At the CEL, we analyze novel approaches based on unsupervised deep learning, which potentially approach maximum likelihood performance. Since its functionality differs from the classical digital signal processing (DSP) blocks, we have to develop metrics and environments for fair comparison. Also, some common ML issues, such as limited training sets, do not apply to communications, so adaptions may be reasonable.
For short channel codes, such as BCH, Reed-Muller and Polar codes, achieving close to maximum likelihood decoding performance using conventional methods is computationally complex. Fueled by the advances in the field of deep learning, belief propagation (BP) decoding can also be formulated in the context of deep neural networks. In BP decoding, messages are passed through unrolled iterations in a feed-forward fashion. Additionally, weights can be introduced
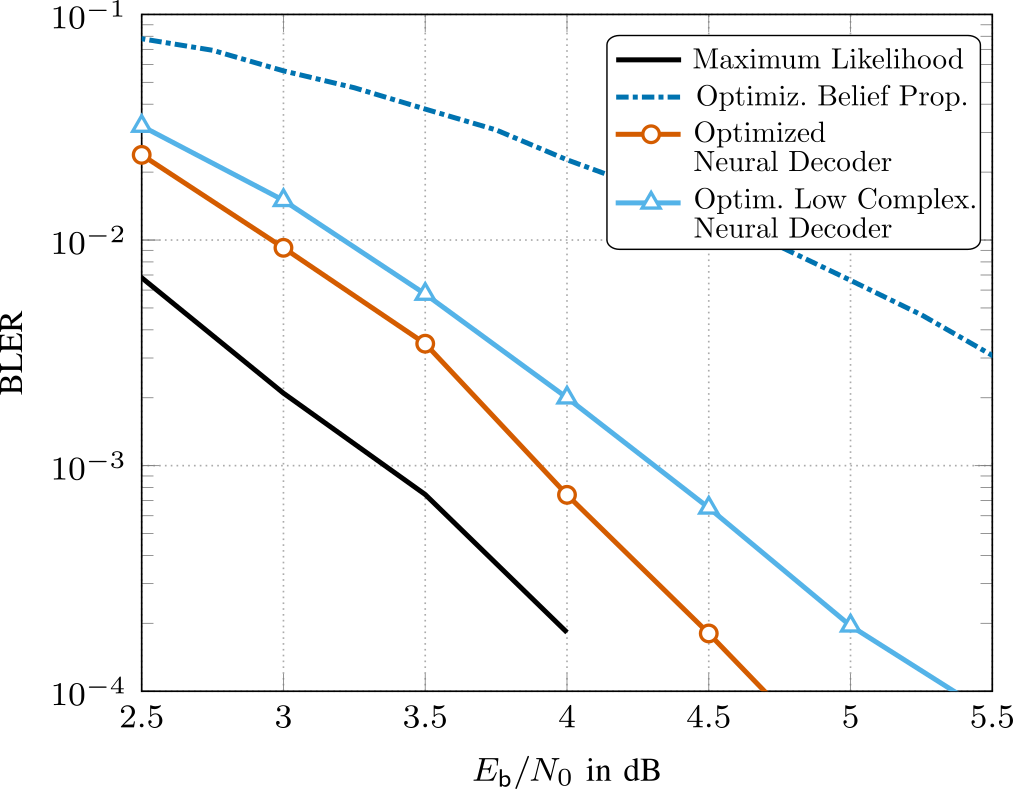
at the edges, which are then optimized using stochastic gradient descent (and variants thereof). This decoding method is commonly referred to as neural belief propagation and can be seen as a generalization of BP decoding, where all messages are scaled by a single damping coefficient. However, the weights add extra decoder complexity. Additionally, in order to achieve competitive performance, overcomplete parity-check matrices are necessary, which further increase decoding complexity. In our research [1], we have employed pruning techniques from ML to significantly reduce decoder complexity and have jointly optimized quantizers for the messages, such that the resulting decoders are directly ready for hardware implementation. The results are shown in Fig. 2, where we see that our optimized decoder operates within 0.5 dB from ML performance. More details can be found in [1].
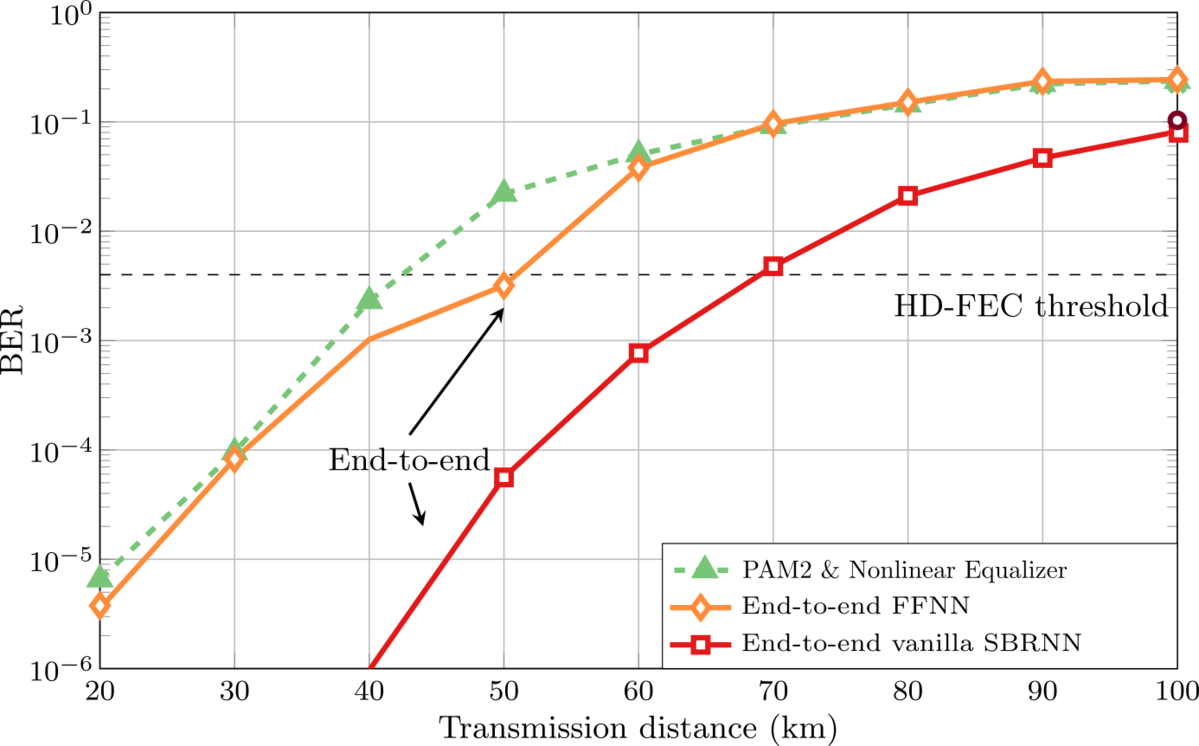
For the design of short-reach optical communication systems based on intensity modulation with direct detection (IM/DD), we may interpret the complete communication chain from the transmitter input to the receiver output as a single neural network and optimize its parameters yielding optimal end-to-end communication performance. In such systems, the combination of chromatic dispersion, introduced inter-symbol interference (ISI), and nonlinear signal detection by a photodiode imposes severe limitations. We have investigated multiple approaches for designing the neural networks [2], [3], including feed-forward and recurrent neural networks. We have shown experimentally that our networks can outperform pulse amplitude modulation (PAM) with conventional linear and nonlinear equalizers (e.g., based on Volterra filters). We have additionally employed Generative Adversarial Networks (GANs) to approximate experimental channels [4]. In Fig. 3, we exemplarily show the bit error rate performance of three such systems (conventional PAM with nonlinear equalizer and two different end-to-end optimized transceivers), where we can observe gains in the range of 20-25km at the FEC threshold.
References
[1] A. Buchberger, C. Häger, H. D. Pfister, L. Schmalen, and A. Graell i Amat, “Pruning Neural Belief Propagation Decoders,” IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, Jun. 2020
[2] B. Karanov, M. Chagnon, F. Thouin, T. A. Eriksson, H. Bülow, D. Lavery, P. Payvel and L. Schmalen, “End-to-end Deep Learning of Optical Fiber Communications,” IEEE/OSA Journal of Lightwave Technology, vol. 36, no. 20, pp. 4843-4855, Oct. 2018, also available as arXiv:1804.04097
[3] B. Karanov, M. Chagnon, V. Aref, F. Ferreira, D. Lavery, P. Bayvel, and L. Schmalen, “Experimental Investigation of Deep Learning for Digital Signal Processing in Short Reach Optical Fiber Communications,” IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, Oct. 2020 (also available on https://arxiv.org/abs/2005.08790)
[4] B. Karanov, M. Chagnon, V. Aref, D. Lavery, P. Bayvel, and L. Schmalen, “Concept and Experimental Demonstration of Optical IM/DD End-to-End System Optimization using a Generative Model,” Optical Fiber Communications Conference (OFC), San Diego, CA, USA, paper Th2A.48, Mar. 2020
Mobilfunknetze
Im Zuge der Entwicklung der 5. Generation des Mobilfunkstandards 3GPP wurden wesentliche Neuerungen eingeführt. Zu den bemerkenswertesten Neuerungen zählen die flexible Skalierbarkeit der physikalischen Übertragungsschicht, die Nutzung von Frequenzen im Millimeterbereich und das überarbeitete Design des Kernnetzes. Die physikalische Schicht des 5G-Standards ermöglicht unterschiedlich lange Symboldauern, wodurch vielfältige Anwendungen mit extremen Anforderungen an Latenz und Datendurchsatz unterstützt werden können. Durch den Einsatz höherer Frequenzen im Millimeterbereich ist es möglich, deutlich höhere Bandbreiten zu nutzen und einen deutlich höheren Datendurchsatz zu erreichen. Dies ist jedoch nur durch den Einsatz von Mehrantennensystemen mit einer großen Anzahl von Antennen möglich, die eine feingranulare Steuerung erfordern. Sämtliche Systemfunktionen wurden im Kernnetz neu definiert, neue Konzepte wie die Trennung von Steuerungs- und Datenebene und Virtualisierung wurden umgesetzt und das Kernnetz kann verschiedene kabelgebundene und kabellose Zugangstechnologien integrieren.
Im Bereich der Mobilfunknetze untersucht das CEL den Systemkontext der Mobilfunkkommunikation, wie moderne Kommunikationsalgorithmen in das System integriert werden können, wie die notwendigen Daten zum Betrieb der Algorithmen bereitgestellt werden können, welche Wechselwirkungen es im Gesamtsystem gibt und wie sich die Netzwerkarchitektur ändern muss, um diese Algorithmen zu unterstützen. Den folgenden Themenbereichen wird besondere Aufmerksamkeit geschenkt.
Optimierung drahtloser Netzwerke und Kommunikationssysteme durch maschinelles Lernen
Im Kontext von 5G wurde erstmals der (standardisierte) Einsatz von KI-Algorithmen in Mobilfunknetzen diskutiert. Am CEL erforschen wir, wie nachrichtentechnische Prozesse mithilfe von KI-Algorithmen verbessert werden können, z.B. Kanalkodierung oder Kanalentzerrer. Andererseits erforschen wir, wie der Betrieb von Mobilfunknetzen mit Hilfe von KI-Algorithmen optimiert werden kann, z.B. Mobilitätsprozesse oder Kommunikationsprotokolle. Neben den eigentlichen Algorithmen untersuchen wir, wie die notwendigen Daten erhoben und gespeichert werden können.
Dynamische und selbstoptimierende drahtlose Netzwerke
Mit den stetig steigenden Anforderungen an Mobilfunknetzen werden auch die eingesetzten Strukturen und Methoden immer komplexer, sodass der Betrieb und die Optimierung des Netzes automatisiert und an das Einsatzszenario angepasst werden müssen. Zu diesem Zweck untersucht das CEL, wie sich das Mobilfunknetz dynamisch an die Anforderungen anpassen kann, z.B. flexible Topologien (drohnengestützte Netzwerke) und resiliente Strukturen sowohl im Funkzugangsnetz als auch im Kernnetz.
Multimodale Kommunikations- und Informationsverarbeitungssysteme
Mobilfunknetze sind mittlerweile stärker an bestimmte Anwendungen gekoppelt, z.B. Automobile oder IoT. Dadurch werden Informationen aus anderen Domänen außerhalb der Mobilkommunikation relevant, z.B. Radarmessungen oder Videoaufzeichnungen. Das CEL untersucht, wie diese Informationen genutzt werden können, um gemeinsam mit der Anwendungsschicht den Betrieb eines Mobilfunknetzes zu optimieren, z.B. in der automatisierten Fernsteuerung von Robotern.
Integration von Kommunikations- und Cyber-Physischen Systemen
Mit dem 5G-Standard wurden auch Anwendungen stärker berücksichtigt, die extreme Anforderungen an Latenz und Zuverlässigkeit stellen. Neben der Dienstqualität auf der Funkschnittstelle ist die Integration in das gesamte Mobilfunksystem inklusive Kernnetz und Anwendung von wesentlicher Bedeutung, da Latenz und Zuverlässigkeit vom „schwächsten“ Glied im gesamten Übertragungsweg dominiert werden. Das CEL erforscht, wie die Integration der verschiedenen Mobilfunkdomänen mit Anwendungen bzw. End-to-End-Anforderungen umgesetzt werden kann.
Software Defined Radio und Cognitive Radio
Die Vision eines Software Radios besteht darin, die kommunikationsspezifische Signalverarbeitung eines Funksystems – wie etwa Modulation, Kanalcodierung oder Kanalentzerrung – so weit wie möglich in Software durchzuführen. In einem idealen Software Radio wird die spezifische Hardware durch einen General Purpose Prozessor in Verbindung mit A/D- und D/A-Wandlern ersetzt. Da die Signalverarbeitung somit nur noch in Form von Algorithmen auf dem GPP erfolgt, entsteht ein Funkgerät, das eine sehr flexible Verwendung erlaubt.
Das Institut für Nachrichtentechnik (CEL) ist seit 1996 in vielfältige SDR-Projekte involviert. Aufbauend auf dieser Erfahrung verfolgt das CEL die Entwicklung von Software Radios hin zu Cognitive Radios. Cognitive Radios stellen eine Erweiterung der Software Radios dar. Bei Cognitive Radios handelt sich um lernende und intelligente Software Radios, die in der Lage sind, ihre spektrale Umgebung zu beobachten und sich somit an aktuelle Gegebenheiten – wie etwa sich verändernde Kanaleigenschaften oder lokal verfügbare Funkstandards – anzupassen.
Durch die umfangreiche Soft- und Hardwareausstattung des CEL ergeben sich vielfältige Möglichkeiten der Forschung im Bereich Software und Cognitive Radio. Modelle und Algorithmen können durch Simulationen untersucht werden. Hierbei stehen umfangreiche Bibliotheken zur Beschreibung von Übertragungssystemen zur Verfügung. Zusätzlich erlaubt die vorhandene Hardware – wie Universal Software Radio Peripheral (USRP) Boards von Ettus Research – das Testen der Algorithmen, indem diese in experimentellen Aufbauten realisiert werden.