Kanalcodierung für die Hochgeschwindigkeitskommunikation
Das fundamentale Problem der Nachrichtentechnik ist es, Information effizient und zuverlässig von einem Punkt (im Raum oder in der Zeit) zu einem anderen Punkt zu transportieren. Beispiele von Systemen der Nachrichtentechnik sind die mobile Kommunikation zwischen Smartphone-Nutzer und Mobilfunkmast, Datenübertragung zwischen Satellit und Bodenstation durch die Atmosphäre und den freien Raum, das Speicher und Lesen von Information in Flash-Speichern und Festplatten, sowie die Vernetzung von Servern in Datenzentren mittels Kupfer- und Glasfaserkabel. Die Übertragung der Daten über ein physikalisches Medium ist unwiederbringlich durch Rauschen (z.B. thermisches Rauschen in Verstärkern) und andere Effekte gestört. Als Konsequenz dieses Rauschens und der Verzerrungen ist das Empfangssignal fehlerhaft.
Um die Fehlerwahrscheinlichkeit zu verringern hat Claude E. Shannon in seiner bahnbrechenden Arbeit gezeigt, dass mithilfe einer sogenannten Kanalcodierung die Fehlerwahrscheinlichkeit beliebig klein werden kann, falls bestimmte Bedingungen erfüllt sind. Das Prinzip der Kanalcodierung ist einfach: Es wird in einer wohldefinierten Art und Weise Redundanz dem Sendesignal hinzugefügt. Diese Redundanz kann am Empfänger gezielt verwendet werden um die durch die Übertragung verursachten Übertragungsfehler zu korrigieren. Dazu muss die Rate des Kanalcodes (diese definiert die Menge an zugefügter Redundanz) unterhalb einer von Shannon eingeführten Größe - der Kanalkapazität - sein. Die Kanalkapazität ist eine fundamentale Größe eines jeden Kanals.
Heutzutage existieren leistungsfähige Kanalcodierverfahren. Die meisten dieser Verfahren basieren auf der Klasse der sogenannten Low-Density Parity-Check (LDPC) Codes. LDPC-Codes wurden schon in den 1960er Jahren eingeführt, sind danach aber weitestgehend in Vergessenheit geraten, da ihre Decodierung für die damaligen Verhältnisse zu aufwändig war. Nach der Erfindung von Turbo-Codes im Jahre 1993 gab es ein neu erwecktes Interesse an iterativ decodierbaren Codes, und die LDPC-Codes wurden wiederentdeckt. In den darauffolgenden Jahren konnte ein tiefgehendes und gründliches Verständnis dieser Codes erarbeitet werden und neue, sehr schnelle und hochparallelisierbare Decodierverfahren wurden entwickelt. Aus diesen Gründen werden LDPC-Codes heute in vielen Anwendungen, wie WiFi 802.11, DVB-S2, 10G Ethernet (10G-BaseT), sowie 5G als Methode der Wahl verwendet.
Kanalcodierung für die Hochgeschwindigkeitsdatenübertragung
In der Hochgeschwindigkeitsdatenübertragung über lange Distanzen (z.B. Glasfaserunterseekabel, optische Glasfasern für das Kernnetz, Mikrowellenverbindungen zur Anbindung entlegener Antennen u.v.m) soll vielfach der erreichbare Codiergewinn (und damit auch der Datendurchsatz) maximiert werden bei gleichzeitig niedriger Decodierkomplexität. Soll ein möglichst hoher Codiergewinn angestrebt werden, sind LDPC-Codes auch in dieser Anwendung eine gute Wahl aufgrund ihrer gut untersuchten theoretischen Eigenschaften und der Verfügbarkeit massiv paralleler Decodierverfahren. Allerdings können LDPC-Codes nie den maximal möglichen Codiergewinn erzielen aufgrund Limitierungen in ihrer Konstruktion.
Vor ungefähr 2 Jahrzehnten wurden LDPC-Faltungscodes eingeführt. Diese Codes verbinden LDPC-Codes mit einer übergeordneten Faltungsstruktur. Die Ursprungsidee war die Kombination der Vorteile von LDPC-Codes und Faltungscodes. Eine ähnliche Idee wurde schon in den 1950er und 1960er Jahren mit dem Konzept rekurrenter Codes verfolgt. Das volle Potential dieser LDPC-Faltungscodes ist erst vor einigen Jahren zum Vorschein gekommen, als realisiert wurde, dass die Leistungsfähigkeit dieser Codes asymptotisch die gleiche Leistungsfähigkeit wie ein optimaler (maximum likelihood) Decoder aufweist. Zur Analyse dieses Effekts wurde eine leicht veränderte Konstruktion eingeführt. Die resultierenden Codes wurden "räumlich verkettete" (engl. spatially coupled) Codes genannt. Der Hauptvorteil dieser Codes ist die Möglichkeit, sehr leistungsfähige Codes zu konstruieren, die nichtsdestotrotz mit einem sehr einfachen gefensterten Decoder decodiert werde können. Aus diesem Grund sind räumlich verkettete LDPC-Codes (SC-LDPC-Codes) erstklassige Kandidaten für zukünftige Hochgeschwindigkeitskommunikationssysteme mit sehr hohen Codiergewinnen.
Das folgende Bild zeigt die Fehlerrate (als Funktion über das Signal-Rausch-Verhältnis), die mit zwei SC-LDPC-Codes erzielt werden kann, im Vergleich mit einem herkömmlichen LDPC-Codes, wie er oft verwendet wird. Alle Codes besitzen eine Rate von 0.8 (dies entspricht einem Overhead von 25% für die Redundanzinformation). Mit einem gefensterten Decoder niedriger Komplexität (dieser weist ungefähr die gleiche Komplexität wie ein LDPC-Decoder auf) kann schon ein signifikanter Codiergewinn gegenüber LDPC-Codes erzielt werden. Ein weiterer Vorteil von SC-LDPC-Codes ist deren Zukunftssicherheit. Ein Erhöhen der Decodierkomplexität führt zu zusätzlichen Gewinnen. Dies ist ein weiteres Argument für deren Einsatz in zukünftigen Nachrichtensystemen: mit einem standardisierten und somit rückwärtskompatiblen Verfahren können in der Zukunft höhere Gewinne erzielt werden, wenn die Möglichkeiten der VLSI-Implementierung die Implementierung komplexerer Decoder erlauben. Wir können auch feststellen dass bei einer Bitfehlerrate von ungefähr 10-15 diese Codes (mit einer Festkommaimplementierung) die von Shannon postulierte Kanalkapazität bis auf unter 1dB annähern.
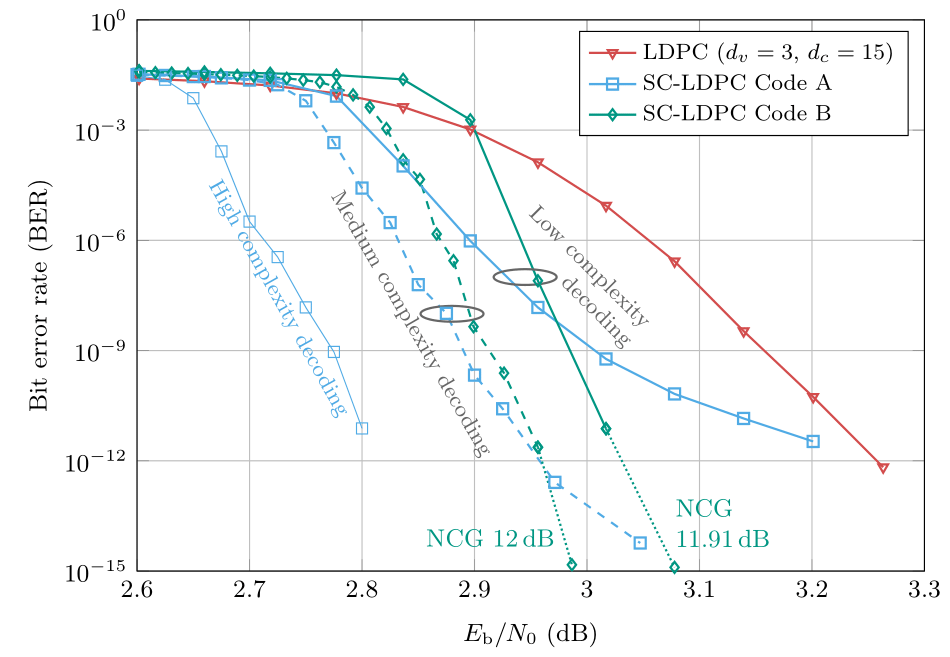
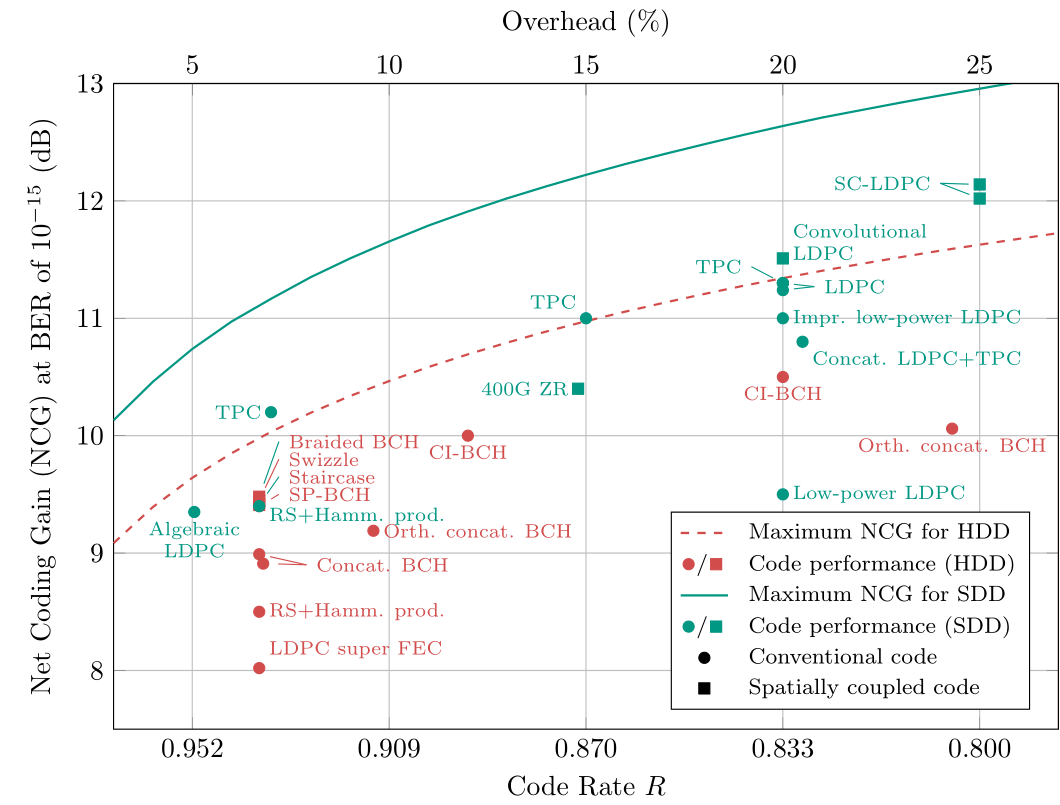
Im folgenden Bild sind die Codiergewinne (sowie deren theoretische Grenzen) für einige Kanalcodierverfahren, wie sie in optischen Nachrichtensystemen verwendet werden, aufgezeigt. Wir unterscheiden zwischen Codes mit Hard-Decision Decodierung (HDD, üblicherweise entworfen für Systeme mit niedriger Empfängerkomplexität) und Codes mit Soft-Decision Decodierung (SDD, üblicherweise entworfen für Systeme mit hohen Codiergewinnen). Eckige Symbole markieren räumlich verkettete Codes. Wir stellen fest, dass die meisten der leistungsfähigsten Codierverfahren solche mit räumlich verketteten Codes sind. Insbesondere SC-LDPC-Codes A und B aus dem vorangegangenen Beispiel haben die höchsten Gewinne.
Forschung zu Kanalcodierung am CEL
Am CEL beschäftigen wir uns mit fundamentalen Fragestellungen zur Kanalcodierung für Hochgeschwindigkeitsdatenübertragungssysteme. Wir entwickeln neue Codierverfahren für niedrige Decodierkomplexität und trotzdem hohen Codiergewinnen. Wir wollen dabei möglichst die Fehlerrate minimieren und berücksichtigen die Eigenschaften des zugrundeliegenden Übertragungssystems, z.B. optische Kanäle oder Mikrowellenlinks. Neben räumlich verketteten Codes untersuchen wir auch die Möglichkeiten alternativer Verfahren, je nach zugrundeliegender Anwendung.
Ausgewählte Literatur:
V. Aref, N. Rengaswamy and L. Schmalen, "Finite-Length Analysis of Spatially-Coupled Regular LDPC Ensembles on Burst-Erasure Channels", IEEE Transactions on Information Theory, vol. 64, no. 5, pp. 3431-3449, May 2018 [IEEE Xplore] [preprint auf arXiv]
L. Schmalen, V. Aref, J. Cho, D. Suikat, D. Rösener, and A. Leven, "Spatially Coupled Soft-Decision Forward Error Correction for Future Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 33, no. 5, pp. 1109-1116, March 2015 [IEEE Xplore]
L. Schmalen, D. Suikat, D. Rösener, V. Aref, A. Leven, and S. ten Brink, "Spatially Coupled Codes and Optical Fiber Communications: An Ideal Match?", IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Special Session on Signal Processing, Coding, and Information Theory for Optical Communications, Stockholm, Sweden, June 2015 [IEEE Xplore] [preprint auf arXiv]
A. Leven and L. Schmalen, "Status and Recent Advances on Forward Error Correction Technologies for Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 32, no. 16, pp. 2735-2750, Aug. 2014 [IEEE Xplore]

